Terminology 術語
https://funatoya.com/funatoka/anatomy/nomina/splanchnologia/urogenitale.htm
尿生殖隆起 Urogenital ridgeの構造
尿生殖隆起 Urogenital ridgeとは何か?というと、もともとは、中間中胚葉です。中間中胚葉 intermediate mesoderm が、発生時期が進んで隆起したものが生殖隆起 Urogenital ridgeです。さらに発生が進むと、nephrogenic cordとgonadal ridgeとに分化します。
- https://abdominalkey.com/embryology-anatomy-and-histology-of-the-kidney/
- https://www.uomosul.edu.iq/public/files/datafolder_117/oldUo_20190821_033023_68_268.pdf この講義資料には、urogenital ridgeやgonadal ridgeなどが明確に示されています。
Urogenital ridge, nephrogenic cord, gonadal ridgeの関係
自分は最初に発生学の教科書を通読したときには、中間中胚葉が尿生殖隆起に分化するという記述を読み落としたみたいで、尿生殖隆起や生殖隆起が唐突に現れたように感じていました。よくよく読むとラーセンの発生学の教科書に、記載がありました。
In addition to the nephric structures, the intermediate mesoderm on both sides of the dorsal body wall gives rise to a gonadal ridge.
Larsen’s Human Embryology
ラーセンではgonadal ridgeという言葉が使われていますが、カールソンの教科書にはgonadal ridgeという言葉は登場せず、代わりにgenital ridgeという言葉が使われていました。こういう言葉のブレも初学者を惑わせます。
ラーセンやカールソンで明確に書かれていないようなことが、ハッキリと書いてあって分かりやすいと思ったのがSinghの教科書です。この図ではmesonephric ridgeのmedial側にgenital ridgeが形成することがわかります。
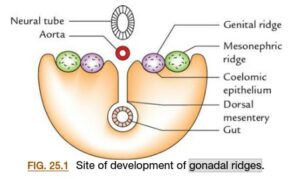 図引用元:Singh, Vishram. Textbook of Clinical Embryology, 3rd Edition
図引用元:Singh, Vishram. Textbook of Clinical Embryology, 3rd Edition
The nephrogenic cord and the urogenital ridge are closely related embryological structures, but they are not exactly the same. Here’s a clear distinction:
🔹 Urogenital Ridge
- A longitudinal elevation of intermediate mesoderm on each side of the dorsal aorta.
- Forms during early embryonic development.
- It gives rise to two major components:
- Nephrogenic cord (or nephrogenic ridge) – related to the urinary system.
- Gonadal ridge – related to the genital (reproductive) system.
🔹 Nephrogenic Cord (Nephrogenic Ridge)
- A part of the urogenital ridge, specifically the lateral portion.
- Gives rise to the three successive kidney structures:
- Pronephros
- Mesonephros
- Metanephros (becomes the permanent kidney)
✅ In summary:
- Nephrogenic cord = urinary portion of the urogenital ridge
- Urogenital ridge = nephrogenic cord (urinary) + gonadal ridge (reproductive)
So, they are related but not synonymous.
(ChatGPT 4o)
The gonadal ridge is a component of the urogenital ridge, specifically its medial portion. Here’s a detailed breakdown of their relationship:
🔷 Urogenital Ridge
- A paired, longitudinal structure derived from the intermediate mesoderm.
- Runs along the dorsal body wall on either side of the dorsal aorta.
- Appears during the 4th week of development.
- Differentiates into two distinct but related ridges:
- Nephrogenic cord (lateral)
- Gonadal ridge (medial)
🔷 Gonadal Ridge
- Forms medially on the urogenital ridge.
- Initially an indifferent structure — not yet male or female.
- Gives rise to the gonads (testes or ovaries), depending on genetic and hormonal influences.
- Involves invasion by primordial germ cells from the yolk sac around the 6th week.
🔄 Relationship
| Feature |
Urogenital Ridge |
Gonadal Ridge |
| Origin |
Intermediate mesoderm |
Medial part of urogenital ridge |
| Function |
Precursor to urinary and reproductive systems |
Precursor to gonads (testis or ovary) |
| Includes |
Nephrogenic cord (lateral) + Gonadal ridge (medial) |
Just the gonadal portion |
| Forms |
Kidneys, gonads, genital ducts |
Only the gonads |
🧠 Key Concept
- The urogenital ridge is a composite structure, and the gonadal ridge is one of its parts.
- Both parts develop in parallel but give rise to different organ systems.
(ChatGPT 4o)
Gonadal ridge(Geniral ridge) 生殖隆起・生殖堤
Does the urogenital ridge run down from head to tail?
- The urogenital system arises fromintermediate mesodermwhich forms aurogenital ridgeon either side of the aorta.
- The urogenital ridge develops into three sets of tubular nephric structures (from head to tail): thepronephros, themesonephros, and themetanephros.
https://embryology.oit.duke.edu/urogenital/urogenital.html
Yes, the urogenital ridge runs from head (cranial) to tail (caudal) along the posterior wall of the embryonic abdominal cavity.
To elaborate:
- The urogenital ridge is a longitudinal elevation of intermediate mesoderm.
- It forms on either side of the dorsal aorta.
- It gives rise to two key structures:
- The nephrogenic cord (lateral part), which develops into the urinary system (kidneys, ureters).
- The gonadal ridge (medial part), which develops into the reproductive organs (testes or ovaries).
So yes — it is an elongated structure that extends craniocaudally, reflecting the segmental development of the embryo.
(ChatGPT 4o)
Yes, the urogenital ridge, a structure in embryonic development, does run from the head to the tail (cranially to caudally) of the developing embryo. This ridge gives rise to both the urinary and genital systems. Specifically, the intermediate mesoderm, which forms the urogenital ridge, develops into three sets of nephric structures (from head to tail): the pronephros, mesonephros, and metanephros.
Here’s a more detailed breakdown:
-
Urogenital Ridge Formation:
The urogenital ridge arises from the intermediate mesoderm, located on either side of the aorta.
-
Cranio-caudal Development:
The three sets of nephric structures (pronephros, mesonephros, and metanephros) develop sequentially from the urogenital ridge, starting from the head (cranial) and progressing towards the tail (caudal) of the embryo.
-
Pronephros:
The first to appear, located in the neck region.
-
Mesonephros:
Located in the mid-section of the embryo, developing into mesonephric tubules and ducts.
-
Metanephros:
The final kidney structure, developing from the caudal end of the mesonephric duct and a condensation of nearby mesoderm.
- 泌尿器系の発生の講義動画 Development of the Urogenital System – Urinary System and Kidney Development by John McLachlan, PhD Urogenital ridgeについての解説 1:39~
- https://app.lecturio.com/#/article/3809
自分:Does the intermediate mesoderm change its name to the urogenital ridge, and further change the name when it turns to three sets of nephric structures (from head to tail): the pronephros, mesonephros, and metanephros?
ChatGPT 4o:
Great question — you’re touching on the dynamic naming and regional specialization of the intermediate mesoderm during development. Here’s a precise explanation:
🌱 1. Intermediate Mesoderm:
- Initially, a longitudinal column of mesoderm located between the paraxial and lateral plate mesoderm.
- It appears bilaterally along the dorsal body wall.
- This structure is simply called intermediate mesoderm in early stages (around week 3–4 of human development).
🪴 2. Urogenital Ridge:
- As development progresses, the intermediate mesoderm bulges into the coelomic cavity, forming the urogenital ridge (starting ~week 4).
- The urogenital ridge is a broader term that includes:
- Nephrogenic cord (lateral part) → forms the urinary system.
- Gonadal ridge (medial part) → forms the genital system.
Yes, you can think of the urogenital ridge as a regionally specified derivative of the intermediate mesoderm.
🌊 3. Pronephros → Mesonephros → Metanephros:
- These are successive nephric structures derived from the nephrogenic cord (i.e., the urinary part of the urogenital ridge), and they appear in a cranial-to-caudal sequence:
| Region |
Structure |
Fate |
| Cranial |
Pronephros |
Rudimentary; regresses quickly |
| Intermediate |
Mesonephros |
Temporary kidney; forms mesonephric duct (Wolffian duct) |
| Caudal |
Metanephros |
Becomes the definitive kidney |
So, in essence:
✅ Intermediate mesoderm →
➡️ Urogenital ridge (as it bulges into body cavity) →
➡️ Nephrogenic cord (for urinary structures) →
➡️ Pronephros → Mesonephros → Metanephros (in sequence, cranial to caudal)
Summary Answer:
Yes, the intermediate mesoderm functionally and regionally transforms — first becoming the urogenital ridge, then differentiating further into specific nephric structures (pronephros, mesonephros, metanephros) along the cranio-caudal axis, as well as the gonadal ridge for the reproductive system.
Let me know if you’d like a diagram to go with this!
その他参考サイト
- https://embryology.med.unsw.edu.au/embryology/index.php?title=Urinary_Bladder_Development
- https://embryology.med.unsw.edu.au/embryology/index.php?title=Urinary_Bladder_Development
- https://v1.pediatricurologybook.com/embryology_urinary_tract.html
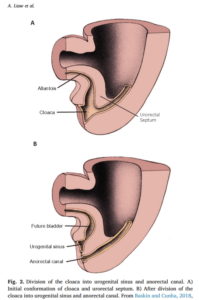 Differentiation 103 (2018) 66–73
Differentiation 103 (2018) 66–73 図引用元:Singh, Vishram. Textbook of Clinical Embryology, 3rd Edition
図引用元:Singh, Vishram. Textbook of Clinical Embryology, 3rd Edition