χ2乗分布は、標準正規分布する確率変数を例えば3個取り出して
X = x1^2 + x2^2 + x3^3 という2乗和をつくったときにXが従う分布です。
自由度は取り出した変数の数で、今の場合3になります。さてこの手順を10000回繰り返して得られる10000個の2乗和がどんな分布を示すかヒストグラムを書いてみますと、
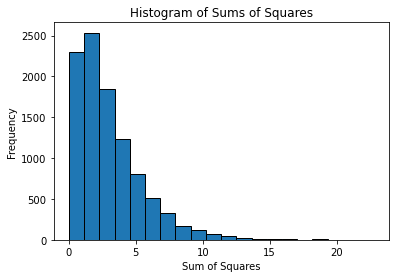
のようになります。なおヒストグラムはpython3で描きました。python3のコードはChatGPT-3.5に作ってもらいました。
上の図が自由度3のχ2乗分布ですが、自由度が1,2,3,4,5,‥とかわったときに分布の形はどう変わるでしょうか。試しに描いてみます。
こんな感じになります。自由度10まで描きました。縦軸はデータ数が10000個のときの度数です。データ数で除算して相対度数で表示すれば、
となります。自由度が大きくなるほどベルシェープ(正規分布)の形に近づいているように見えます。試しに自由度1000にして、サンプル数100000個のヒストグラムを描いてみます。
どうやらこれは正規分布に近い形ですね。今の場合自由度=1000ですが、それが平均値になっているようです。さらに自由度10000にしてみると(サンプル数100000個)、
これくらい自由度を大きくすると、綺麗に左右対称になりました。
自由度kが十分に大きいときカイ二乗分布XはN(k,2k)に収束する
(【統計学】カイ二乗分布の正規近似 自由度が無限大のときのカイ二乗統計量 2022年12月23日 ウサギさんの統計学サロン)
やっぱりそうなんですね。プログラムでいろいろ描いてやると、こういったことが簡単にわかって面白いです。プログラミングは、勉強の道具として最高だと思います。自分はプログラミングはほとんどできないのですが、ゼロからこういったコードを書ける必要がもはや全くなくなりました。生成AIの代表格であるChatGPTさまさまです。「こんなことをしてくれるコードをちょうだい。」と投げるだけで、(多くの場合)完全に動くコードを返してもらえます。凄い時代が来たものです。
今は標準正規分布から変数を取り出しましたが、「標準」でない正規分布N(μ, σ^2)の場合はどうすればよいかというと、X-μ / σ という変数を考えれば、これは標準正規分布に従うので、X-μ / σ の2乗和がχ2乗分布に従うことになります。