ベクトルデータがあるとき、そのベクトルをクラスターに分けたいことがあります。ベクトルといっても、1次元すなわちただの数値の集まりでも構いません。2次元でも3次元でも数十次元でも構いません。例えば多数の車種を分類したければ、ベクトルとして、(価格、燃費、排気量、生産台数、などなど)などが考えられます。大学の分類をしたければ、(学生数、科研費採択数、などなど)でもいいでしょう。動物の動く速さを1000回測定したものでもいいかもしれません。もしその動物の動きのモードが、歩く、走る、突っ走る、の3つなら、動く速さの数値は3つにクラスタリングされるだろうと思います。
k-平均クラスタリングはどんな用途で使われるのか
了解、もっと “現場で具体的にどう使われているか” の一覧ですね。専門的理屈は最小限にして、分野 / 具体タスク / 目的(なぜ k‑means) をテンポよく並べます。
1. マーケティング・ビジネス
| 具体例 | 目的 |
|---|---|
| 顧客セグメンテーション(購買金額×頻度×カテゴリ多様性など) | 似た購買行動の顧客群に分けて施策内容・メール内容を変える |
| 解約(離脱)パターン抽出 | “離脱前に現れる行動プロファイル” 群を見つけ早期介入 |
| 広告クリエイティブ評価ログ(クリック率特徴量) | 類似パフォーマンス広告をまとめ A/B テスト設計を効率化 |
2. 金融
| 具体例 | 目的 |
|---|---|
| 投資家取引スタイル(保有期間、回転率、ボラ耐性) | スタイル別リスク管理・レコメンド |
| 企業財務指標クラスタ(ROE, 負債比率, 成長率…) | ピアグループ比較・異常値検知の基準作り |
| 不正利用前のカード利用パターン “正常クラスタ” 学習 | 正常クラスタからの逸脱度を異常スコア化(前処理) |
3. 医療・生命科学
| 具体例 | 目的 |
|---|---|
| 患者バイタル / 血液検査の時系列特徴を集約した統計 | 臨床表現型サブグループ(治療反応性が違う集団)探索 |
| 遺伝子発現(マイクロアレイ、RNA-seq)で遺伝子をクラスタ | 共発現モジュール → 機能注釈 GO 解析の対象セット作成 |
| 代謝物質濃度プロファイル | 疾患サブタイプ候補の粗い層別化(後で精査) |
| 医用画像のパッチ色・テクスチャ特徴 | 病変候補領域と背景を粗分類(後工程 CNN に渡す) |
4. 画像・コンピュータビジョン
| 具体例 | 目的 |
|---|---|
| 減色(カラー量子化):写真を k 色に圧縮 | PNG/JPEG サイズ削減・スタイル化 |
| Bag of Visual Words:SIFT / ORB 特徴を k‑means | “コードブック” 生成 → 画像分類の入力ベクトル化 |
| 動画内フレームの代表抽出(フレーム特徴) | サムネイル自動選択・冗長フレーム除去 |
5. テキスト・NLP
| 具体例 | 目的 |
|---|---|
| 文書/ニュース記事の埋め込み(BERT など)をクラスタ | トピック群の粗分類・要約(各クラスタ代表文) |
| FAQ ログ(質問埋め込み)クラスタ | 似た質問を束ねテンプレ回答を整備 |
| 顧客サポート問い合わせの分類(ラベル不足時) | 優先的に人手ラベル付けする “代表クラスター” 選定 |
6. 推薦・パーソナライズ
| 具体例 | 目的 |
|---|---|
| ユーザー行動特徴(閲覧ジャンル分布、滞在時間) | k 個のユーザープロフィール類型 → コールドスタート推薦 |
| アイテム特徴ベクトル(コンテンツ埋め込み) | 類似アイテムクラスタの “代表” を使い探索空間を縮小 |
7. IoT / センサ・製造
| 具体例 | 目的 |
|---|---|
| 機械振動スペクトルの特徴量クラスタ | 稼働モード(通常運転、低負荷、高負荷)区別 → 異常検知基準 |
| 電力消費パターン(1 日の 24h プロファイル) | 消費行動タイプ別の需要予測モデル分岐 |
| 製造ライン品質検査の寸法データ | 正常品クラスタ中心 → 外れた個体を二次検査へ |
8. 交通・地理情報
| 具体例 | 目的 |
|---|---|
| GPS 移動軌跡から抽出した “滞在地点” をクラスタ | 代表的滞在場所(自宅/職場/店舗群)の自動識別 |
| 都市内タクシー乗車地点(緯度経度→埋め込み) | 需要ホットスポット分類 → 配車最適化 |
| 気象観測局の長期統計値 | 類似気候ゾーン分け(中規模地域分類) |
9. 教育・eラーニング
| 具体例 | 目的 |
|---|---|
| 学習ログ(解答時間、復習間隔、正答率推移) | 学習行動タイプ(集中型・こつこつ型)で介入策差別化 |
| コース受講者の課題提出遅延パターン | リスククラスターを早期アラート |
10. サイバーセキュリティ
| 具体例 | 目的 |
|---|---|
| ネットワークフローの統計特徴(バイト数、方向比率) | “通常” の通信タイプ群を定義 → 新種挙動を外れとして監視 |
| ログイン時刻×IP 地理情報 | 典型ログインパターン群 → 異常シーケンス検出 |
11. SNS / 行動解析
| 具体例 | 目的 |
|---|---|
| ユーザーの投稿頻度・反応率・活動時間帯 | アクティビティ類型(夜型拡散型など)把握 |
| フォロー関係を埋め込み(node2vec など)後クラスタ | コミュニティ抽出(ラベル無しの “興味圏” 推定) |
12. サプライチェーン・オペレーション
| 具体例 | 目的 |
|---|---|
| SKU の需要時系列から特徴(季節性指標、変動係数)抽出 | 類似需要パターンごとに在庫戦略を分岐 |
| 納期遅延やリードタイム統計 | “安定”“揺らぎ” サプライヤ群を分類 |
なぜ “k‑means がまず試される” のか(共通理由)
- 高速:大規模データでとりあえず構造をざっくり見る初手。
- 結果が説明しやすい:各クラスタ中心=“典型的プロファイル” として共有しやすい。
- 後工程に使い回しやすい:圧縮(代表点)、初期ラベル、特徴エンコード(距離を新特徴に)など応用が広い。
- 実装・運用が単純:パラメータは基本 k と初期化回数くらい。
超短い要約
顧客分け・患者サブタイプ・センサ稼働モード・画像/テキストの代表パターン抽出・需要/行動タイプ分類 といった “似たものをまとめて代表を得たい” ほとんどの初期探索場面でまず k‑means が叩かれる。
kはどうやって決めるのか
自分:k-means法(クラスタリング)って、kは自分で指定するんだっけ?いくつのクラスタに分かれるかわからない場合の手法は何?
ChatGPT 3o:
はい。
1. k‑means 法について
k‑means は「データを ちょうど k 個 のクラスタに分ける」ことを前提にした手法です。したがって k はユーザがあらかじめ決めて入力 します。k を変えると結果も変わるため、適切な k を選ぶ工夫が必要になります。
2. k を事前に知らない場合の代表的アプローチ
| アプローチ | 概要 | 長所 | 主な注意点 |
|---|---|---|---|
| (A) 評価指標を用いて k を後から選ぶ | k を 1, 2, … と変えてクラスタリングを繰り返し、以下のような指標が最適化される k を選ぶ | 実装が容易(k‑means をそのまま使える) | 「最適 k」が必ずしも明確に現れないデータもある |
| • エルボー法 | SSE(クラスタ内平方和誤差)の減りが鈍化する点を探す | 直感的 | 目視判断なので曖昧さが残る |
| • シルエット係数 | 各点が同クラスタにどれだけ適合しているかを −1〜1 で評価 | ノイズに比較的強い | 高次元・大規模データでは計算コスト増 |
| • Gap Statistic | SSE を無作為分布の期待値と比較 | 理論的裏付けがある | 実装がやや手間 |
| (B) k を要しないクラスタリング手法を選ぶ | アルゴリズム自体がクラスタ数を推定、または“しきい値”で決まる | k の指定が不要 | 代わりに他のハイパーパラメータが必要なことが多い |
| • DBSCAN / OPTICS | 密度が高い領域をクラスタとみなし、孤立点を外れ値と扱う | 形状が非球面でも OK・外れ値検出可 | ε(近傍半径)と minPts の調整が鍵 |
| • Mean‑Shift | カーネル密度推定でモード(ピーク)を検出 | k 不要・パラメータは帯域幅のみ | 高次元・大規模データで計算量大 |
| • 階層的クラスタリング(凝集 / 分割) | デンドログラムを任意の高さでカット | 途中経過の可視化が容易 | 距離尺度の選択で結果が大きく変わる |
| • Affinity Propagation | “代表点” を競合的に選びクラスタ生成 | k 不要 | 収束しない場合がある・計算コスト高 |
| (C) モデルベース・ベイズ的手法 | データ生成モデルと尤度(または事前分布)に基づきクラスタ数を推定 | 統計的厳密性 | 計算が重い・実装複雑 |
| • Gaussian Mixture Model+情報量規準(AIC/BIC) | k を変えて推定→最小 AIC/BIC を選択 | GMM が分布仮定に合わないと不適 | |
| • Dirichlet Process GMM(非パラメトリック) | k→∞ の極限で自動的に有限個に収束 | 完全に k 不要 | ハイパーパラメータと MCMC/VI の収束管理 |
3. 実務的な選択ガイド
- 計算コスト・スケールが最優先 ―― 大規模・高次元データなら
- k‑means+シルエット or エルボー で素早く試行
- 複雑な形状/外れ値の影響が大きい ―― 非線形クラスタを想定するなら
- DBSCAN / OPTICS / Mean‑Shift
- 確率モデルで不確実性も評価したい ―― 統計的厳密性が必要なら
- GMM+BIC / Dirichlet Process GMM
- クラスタ間・階層構造を可視化したい ――
- 階層的クラスタリングでデンドログラムを利用
まとめ
- k‑means は「クラスタ数を決め打ちする」アルゴリズム であり、未知の場合は k を評価指標で調整 するか、k 不要のクラスタリング手法 を採用します。
- データの規模・形状・目的(解釈重視か高速性重視か)に応じて手法を選択し、必要に応じてハイパーパラメータを交差検証すると、より頑健なクラスタ分割が得られます。
自分:k=3以上の値を決めているのに、2群になるということはある?ま、データがそもそも2群だったら、そうなるよね?
ChatGPT 3o:
結論から言うと 「名目上は k 個のクラスタが出来る」 のが k‑means の仕様ですが,
実質的に 2 群しか存在しないように見える ケースは珍しくありません。原因はおおむね次の3つです。
1. 「空クラスタ」問題と実装の挙動
- k‑means の反復過程では,あるステップで どのデータ点も割り当てられない重心(=空クラスタ) が生じることがあります。
- 多くのライブラリ(scikit‑learn, MATLAB など)は 空になった重心をランダム再初期化 して反復を続行する設計なので,最終的には 必ず k 個のラベル が返ります。
- ただし再初期化後も収束時に 2 個の重心がほぼ同じ位置に落ち着くことがあり,結果として「実質 2 群」のように見える場合があります。
ポイント:実装が「空クラスタをどう扱うか」で
- 厳密に k 個 に拘束する(通常のライブラリ)
- 空クラスタを許容しそのまま終了(オリジナル実装や学習用コード)
の2タイプがあり,後者だとラベルが2つしか残らないことも起こり得ます。
2. データ分布が本当に 2 群しかない
- ご指摘のとおり,真の構造が 2 群 しかなければ,k>2 にしても 余計な重心が同じ群内で分裂 するだけです。
- その場合,エルボー法やシルエット係数で 「k=2 で最適」 というシグナルが出るのが普通です。
3. 対称配置や重心の初期化で“重複”解に落ちる
- データが左右対称・環状などの場合や,k‑means++ の初期化で たまたま近接した重心が選ばれる と,
2 つの重心がほぼ同一点に収束 → 実質 1 群扱いになることがあります。 - これを避けるには
- 複数回(n_init を増やす) 走らせて最良解を選ぶ
- PCA による次元削減後にクラスタリング
- DBSCAN など k 不要の手法で“地ならし”してから k‑means を適用
といった工夫が有効です。
まとめ
- 理屈上 k‑means は k 個の重心を返すが,
- ライブラリの再初期化で「ラベルは k,実質は 2 群」
- 再初期化しない実装で「ラベル自体が 2 つ」
という両パターンが起こり得る。
- 真のクラスタ数が 2 しかないと判断されるなら,評価指標を用いて k=2 に戻すか,クラスタ数を自動推定する DBSCAN・GMM+ BIC などに切り替えるのが常道です。
自分:k-means clusteringのデモを頂戴。自分で走らせたいから。
ChatGPT 3o:
使い方メモ
| 手順 | 内容 |
|---|---|
| ① 依存関係 | pip install scikit-learn matplotlib |
| ② k の変更 | k = <好きな値> で何度でも試行 |
| ③ データ差し替え | X を自前データ(NumPy 配列/Pandas DataFrame)に置換 |
| ④ 評価指標 | silhouette_score のほか、エルボー法用に SSE(kmeans.inertia_)も取得可 |
| ⑤ 再現性 | random_state を固定すると毎回同じ初期化で比較しやすい |
-
n_init=10は初期重心を 10 回ランダムに振り直し、最良解を採用する安全策です。 -
k を 1~10 までループ → silhouette 係数または SSE をプロットすれば エルボー法/シルエット分析 の定型グラフが作れます。
-
真のクラスタ形状が非球面・密度不均一なら、DBSCAN や 階層クラスタリング と比較してみると理解が深まります。
お好みに応じて拡張してみてください。Happy clustering!
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# ---- 1. サンプルデータ生成(今回の例は 4 つの真クラスタ) ----
X, y_true = make_blobs(n_samples=300,
centers=4,
cluster_std=0.60,
random_state=0)
# ---- 2. k‑means 実行 ----
k = 4 # ★← ここを書き換えてクラスタ数を試行
kmeans = KMeans(n_clusters=k, n_init=10, random_state=0)
labels = kmeans.fit_predict(X)
centers = kmeans.cluster_centers_
# ---- 3. 妥当性指標(シルエット係数) ----
sil = silhouette_score(X, labels)
# ---- 4. 可視化 ----
plt.figure(figsize=(6, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, s=30) # データ点
plt.scatter(centers[:, 0], centers[:, 1],
s=200, marker="X") # クラスタ中心
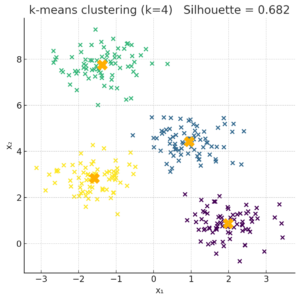
plt.title(f"k‑means clustering (k={k}) "
f"Silhouette = {sil:.3f}")
plt.xlabel("x₁")
plt.ylabel("x₂")
plt.tight_layout()
plt.show()
# ---- 5. 中心座標の確認 ----
print("Cluster centers:\n", centers)
そもそもkはどうやって決めるのか?
クラスタの数kは自明ではないでしょうし、目で見てあきらかに2つとか3つだったとしても、客観的にその妥当性を示さないと論文にしづらいでしょう。kはいくつが最適なのかを客観的に決める方法として、エルボー法やシルエット法といったものがあるそうです。
エルボー法で最適なkを決める
客観的なエルボーの検出法:2次元ベクトル間の角度(Kneedleアルゴリズムの簡易版)
手順:
-
始点(k=1)と終点(k=max)を結ぶ直線を作成
-
各点(k, SSE)からこの直線への垂直距離を計算
-
最大距離の点が「肘」(=最も曲がっている点)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# サンプルデータ生成
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# SSE計算
sse = []
K_range = range(1, 11)
for k in K_range:
kmeans = KMeans(n_clusters=k, n_init=10, random_state=0)
kmeans.fit(X)
sse.append(kmeans.inertia_)
# ---- 肘の自動検出アルゴリズム ----
# 線分の始点と終点
x = np.array(list(K_range))
y = np.array(sse)
point1 = np.array([x[0], y[0]])
point2 = np.array([x[-1], y[-1]])
# 各点と直線 point1-point2 の距離を求める
def distance_to_line(point, line_start, line_end):
return np.abs(np.cross(line_end - line_start, line_start - point)) / np.linalg.norm(line_end - line_start)
distances = [distance_to_line(np.array([x[i], y[i]]), point1, point2) for i in range(len(x))]
elbow_k = x[np.argmax(distances)]
# ---- プロット ----
plt.figure(figsize=(6, 4))
plt.plot(x, y, marker='o', label='SSE')
plt.plot([point1[0], point2[0]], [point1[1], point2[1]], '--', color='gray', label='Base Line')
plt.scatter(elbow_k, sse[elbow_k - 1], s=200, color='red', marker='X', label=f"Elbow at k={elbow_k}")
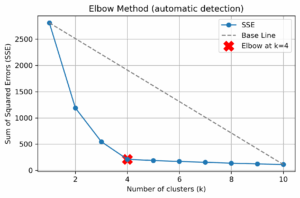
plt.title('Elbow Method (automatic detection)')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Sum of Squared Errors (SSE)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
print(f"エルボー法で推定される最適なクラスタ数: k = {elbow_k}")
上のコードの実行結果
シルエット法で最適なkを決める
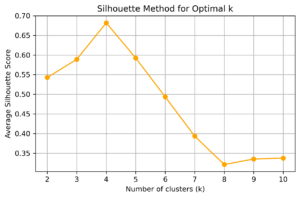
シルエット法(Silhouette Method) 目的:クラスタ数 k を変化させて、シルエット係数の平均値をプロット。値が高いほどクラスタ分けの良さが示される。
silhouette_avgs = []
K_range = range(2, 11) # Silhouetteはk=2以上で意味あり
for k in K_range:
kmeans = KMeans(n_clusters=k, n_init=10, random_state=0)
labels = kmeans.fit_predict(X)
sil = silhouette_score(X, labels)
silhouette_avgs.append(sil)
# プロット
plt.figure(figsize=(6, 4))
plt.plot(K_range, silhouette_avgs, marker='o', color='orange')
plt.title('Silhouette Method for Optimal k')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Average Silhouette Score')
plt.grid(True)
plt.tight_layout()
plt.show()
結果
エルボー法とシルエット法のどちらを使うべきか
シルエット法とエルボー法はどちらもクラスタ数
の最適値を決めるためのクラスタリング妥当性指標ですが、それぞれに特徴・長所・限界があります。以下に比較と使い分けをわかりやすく整理します。
🧭【要約】使い分けのガイドライン
| 観点 | エルボー法 | シルエット法 |
|---|---|---|
| 基準 | クラスタ内誤差(SSE) | クラスタの分離と密度 |
| 出力 |
によるSSEの変化 |
各
に対するスコア(-1〜+1) |
| 最適な
の指標 |
SSEが急に下がらなくなる「肘」 | シルエットスコアが最大の
|
| クラスタの形状への感度 | 球状クラスタに強い(KMeans向き) | 非球状・異なる密度にもある程度対応 |
| 計算コスト | 低い | 高い(すべての点の距離を計算) |
| 明確さ | エルボーが不明瞭な場合もある | より明確なピークが出やすい |
| 実務での使い方 | 初期の探索に向く | 最終判断や評価に向く |
🔍 エルボー法の特徴
- **SSE(クラスタ内平方和誤差)**がどれだけ減るかを見て、
- 減少が鈍る「肘(elbow)」が最適なクラスタ数の候補。
- KMeans向けに設計された理論で、クラスタが球状に分布する場合に有効。
- ただし、「肘」がはっきりしないデータでは使いにくい。
✔ 向いているケース:
- 高速におおまかな候補を探したい
- 明らかにクラスタが分かれている(球状)場合
🔍 シルエット法の特徴
- 各点の「クラスタ内の凝集度」と「他クラスタとの分離度」を評価。
- スコアが高いほどよいクラスタ分け(最大値が最適k)。
- 計算に時間がかかるが、分離が良く、クラスタの一貫性が高いkを推定できる。
✔ 向いているケース:
- 精度重視のとき(論文や実用システム)
- クラスタ形状が不均一/非球状な可能性があるとき
- クラスタ数を細かく調べたいとき
🎯 具体的な使い方(併用がベスト)
- エルボー法で、SSEが急減しなくなる「候補の範囲(例:3〜6)」を絞る
- シルエット法で、その中から最もスコアが高い
を選ぶ
🧠 補足:他の方法と併用
- Gap Statistic(ギャップ統計量):統計的に有意な
を推定
- Calinski-Harabaszスコア:クラスタ間とクラスタ内分散の比
- Davies-Bouldin指標:小さいほど良いクラスタ分け(分離 + 凝集)
✅ 結論:どちらを使うか?
- 手軽におおまかな目安を得たい → エルボー法
- 明確な評価と最適解が欲しい → シルエット法
- クラスタ数に強い確信を持ちたい → 両方使う
(ChatGPT 3o)